Underwater Image Enhancement using Multi-Scale Fusion
Abstract
This project describes a novel strategy to enhance underwater images. Built on the fusion principles, our strategy derives the inputs and the weight measures only from the degraded version of the image. In order to overcome the limitations of the underwater medium we define two inputs that represent color corrected and contrast enhanced versions of the original underwater image, but also four weight maps that aim to increase the visibility of the distant objects degraded due to the medium scattering and absorption. Our strategy is a single image approach that does not require specialized hardware or knowledge about the underwater conditions or scene structure. Our fusion framework also supports temporal coherence between adjacent frames by performing an effective edge preserving noise reduction strategy. The enhanced images are characterized by reduced noise level, better exposedness of the dark regions, improved global contrast while the finest details and edges are enhanced significantly. In addition, the utility of our enhancing technique is proved for several challenging applications. The enhanced images are characterized by reduced noise level (verified by PSNR), better exposedness of the dark regions and improved global contrast. Experimental validity of our method is done by qualitative and quantitative analysis on several images using image quality index -- Entropy and Contrast Improvement Index (CII).
1. Introduction
Underwater things are less visible because of lower levels of natural illumination caused by rapid attenuation of light with distance passed through the water, the reflected light is scattered and as a result, distant objects and parts of the underwater scene are less visible, which is characterized by reduced contrast and faded colors. These effects vary with wavelength of the light, and color and turbidity of the water.
Restoration of images taken in these specific conditions has caught increasing attention. This task is important in several application such as object recognition and intelligent submarines.
Multi-image techniques solve this problem by processing several input images, that have been taken in different conditions. Another alternative is to assume that an approximated 3D geometrical model of the scene is given. A more challenging problem is when only a single degraded
image is available.
1.1 Introduction to Problem
Underwater visibility has been typically investigated by involving acoustic imaging and optical imaging systems. Acoustic sensors have the major advantage to penetrate water much easily despite of their lower spatial resolution in comparison with the optical systems. However, acoustic sensors become very large when aiming for high resolution outputs. On the other hand, optical systems despite of several shortcomings such as poor underwater visibility, have been applied recently by analyzing the physical effects of visibility degradation. Mainly, the existing techniques employ several images of the same scene registered with different states of polarization for underwater images but as well for hazy inputs. As well, dehazing techniques have been related with the underwater restoration problem but in our experiments these techniques shown limitations to tackle with this problem.
A novel approach is introduced that is able to enhance underwater images based on a single image. This approach is built on the fusion principle. In contrast to other methods, this fusion-based approach does not require multiple images, deriving the inputs and the weights only from the original degraded image. Since the degradation process of underwater scenes is both multiplicative and additive traditional enhancing techniques like color balance, color correction, histogram equalization shown strong limitations for such a task. Instead of directly filtering the input image, we used a fusion-based scheme driven by the intrinsic properties of the original image (these properties are represented by the weight maps). The success of the fusion techniques is highly dependent on the choice of the inputs and the weights and therefore we investigate a set of operators in order to overcome limitations specific to underwater environments. As a result, in our framework the degraded image is firstly white balanced in order to remove the color casts while producing a natural appearance of the sub-sea images. This partially restored version is then further enhanced by suppressing some of the undesired noise. The second input is derived from this filtered version in order to render the details in the entire intensity range.This fusion based enhancement process is driven by several weight maps. The weight maps of our algorithm assess several image qualities that specify the spatial pixel relationships. These weights assign higher values to pixels to properly depict the desired image qualities. Finally, this process is designed in a multi-resolution fashion that is robust to artifacts. Different than most of the existing techniques.
A novel approach is introduced that is able to enhance underwater images based on a single image. This approach is built on the fusion principle. In contrast to other methods, this fusion-based approach does not require multiple images, deriving the inputs and the weights only from the original degraded image. Since the degradation process of underwater scenes is both multiplicative and additive traditional enhancing techniques like color balance, color correction, histogram equalization shown strong limitations for such a task. Instead of directly filtering the input image, we used a fusion-based scheme driven by the intrinsic properties of the original image (these properties are represented by the weight maps). The success of the fusion techniques is highly dependent on the choice of the inputs and the weights and therefore we investigate a set of operators in order to overcome limitations specific to underwater environments. As a result, in our framework the degraded image is firstly white balanced in order to remove the color casts while producing a natural appearance of the sub-sea images. This partially restored version is then further enhanced by suppressing some of the undesired noise. The second input is derived from this filtered version in order to render the details in the entire intensity range.This fusion based enhancement process is driven by several weight maps. The weight maps of our algorithm assess several image qualities that specify the spatial pixel relationships. These weights assign higher values to pixels to properly depict the desired image qualities. Finally, this process is designed in a multi-resolution fashion that is robust to artifacts. Different than most of the existing techniques.
1.2 Figure
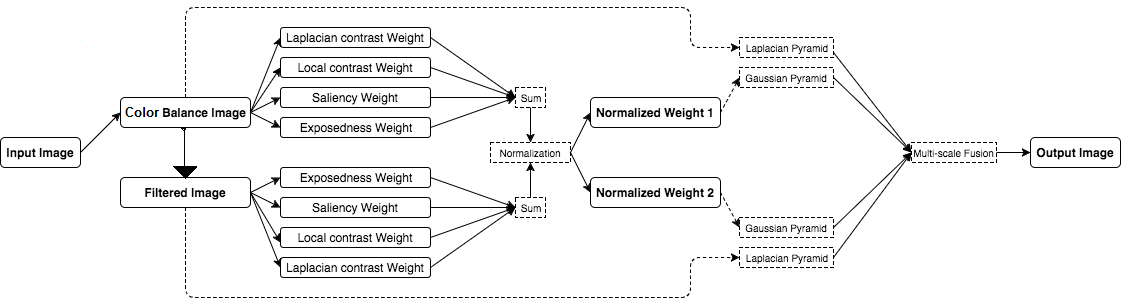
Figure 1: Functional Block Diagram


1.3 Literature Review
Enhancing images represents a fundamental task in many image processing and vision applications. As a particular challenging
case, restoring hazy/underwater images requires specific strategies and therefore an important variety of methods have emerged to solve this problem. Firstly, several contrast enhancement techniques have been developed for remote sensing systems, where the input information is given by a multi-spectral imaging sensor installed on the Landsat satellites. The recorded six-bands of reflected light are processed by different strategies in order to yield enhanced output images. The well-known method of Chavez is suitable for homogeneous scenes, removing the haziness by subtracting an offset value determined by the intensity distribution of the darkest object.
Zhang et al. introduced the haze optimized transformation (HOT), using the blue and red bands for haze detection, that have been shown to be more sensitive to such effects. Moro and Halounova generalized the dark object subtraction approach for highly spatially-variable haze conditions. A second category of methods, employs multiples images or supplemental equipment. In practice, these techniques use several input images taken in different conditions. Their main drawback is due to their acquisition step that in many cases is time consuming and hard to carry out.
We have implemented following paper for this project- "Enhancing Underwater Images and Videos by Fusion" -- Cosmin Ancuti, Codruta Orniana Ancuti, Tom Haber and Philippe Bekaert Hasselt University - tUL -IBBT, EDM, Belgium. Published in: Computer Vision and Pattern Recognition (CVPR), 2012 IEEE Conference on 26 July 2012. The link to the page can be found - here.
Zhang et al. introduced the haze optimized transformation (HOT), using the blue and red bands for haze detection, that have been shown to be more sensitive to such effects. Moro and Halounova generalized the dark object subtraction approach for highly spatially-variable haze conditions. A second category of methods, employs multiples images or supplemental equipment. In practice, these techniques use several input images taken in different conditions. Their main drawback is due to their acquisition step that in many cases is time consuming and hard to carry out.
We have implemented following paper for this project- "Enhancing Underwater Images and Videos by Fusion" -- Cosmin Ancuti, Codruta Orniana Ancuti, Tom Haber and Philippe Bekaert Hasselt University - tUL -IBBT, EDM, Belgium. Published in: Computer Vision and Pattern Recognition (CVPR), 2012 IEEE Conference on 26 July 2012. The link to the page can be found - here.
1.4 Proposed Approach
The proposed technique is described by three main steps. Firstly, we derive the sequence of input images characterized by the desired details that need to be preserved in the restored result. Secondly, the weight maps that rate the locally important information are defined and finally, the composition of the final output is obtained by employing a classical multi-scale fusion strategy. An important advantage is that by our strategy the underwater image enhancement may be performed reliably even when the distance map (transmission) is not previously estimated.
In short, Our enhancing strategy consists of three main steps: inputs assignment (derivation of the inputs from the original underwater image), defining weight measures and multiscale fusion of the inputs and weight measures.
In short, Our enhancing strategy consists of three main steps: inputs assignment (derivation of the inputs from the original underwater image), defining weight measures and multiscale fusion of the inputs and weight measures.
1.5 Report Organization
The rest of the description follows the following organisation: Section 2 describes the detailed approach followed to get the enhanced underwater image. Section 3 shows our experiment results and the data set used for verifying. In section 4, we sumarised the result and conclude that image is indeed enhanced by looking at it visually as well as using quantitative image quality indexes such as Entropy and Contrast Image Improvement (CII). We also verified that the noise has been reduced in the enhanced output using PSNR. Finally, We conclude our project by stating some applications of our implemented method.
2. Proposed Approach
In this work we showed an alternative single image based solution built on the multi-scale fusion principles. We aim for a simple and fast approach that is able to increase the visibility of a wide variation of underwater videos and images. Our framework blends specific inputs and weights carefully chosen in order to overcome the limitation of such environments. For the most of the processed images shown in Image Dataset, the back-scattering component (yielded in general due to the artificial light that hits the water particles and then is reflected back to the camera) has a reduced influence. This is generally valid for underwater scenes decently illuminated by natural light. However, even when artificial illumination is needed, the influence of this component can be easily diminished by modifying the angle of the source light. Our enhancing strategy consists of three main steps: inputs assignment (derivation of the inputs from the original underwater image), defining weight measures and multi scale fusion of the inputs and weight measures.
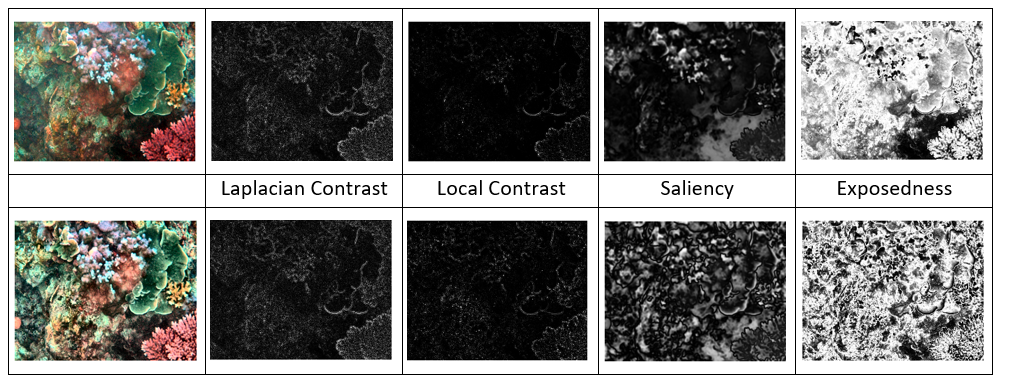
2.1 Inputs of the Fusion Process
When applying a fusion algorithm the key to obtain good visibility of the final result is represented by the well tailored inputs and weights. Different than most of the existing fusion methods, this fusion technique processes only a single degraded image. The general idea of image fusion is that the processed result, combines several input images by preserving only the most significant features of them. Thus, results obtained by a fusion-based approach fulfills the depiction expectation when each part of the result presents an appropriate appearance in at least one of the input images. In this single-based image approach two inputs of the fusion process are derived from the original degraded image.
This enhancing solution does not search to derive the inputs based on the physical model of the scene, since the existing models are quite complex to be tackled. The first derived input is represented by the color corrected version of the image while the second is computed as a contrast enhanced version of the underwater image after a noise reduction operation is performed.
This enhancing solution does not search to derive the inputs based on the physical model of the scene, since the existing models are quite complex to be tackled. The first derived input is represented by the color corrected version of the image while the second is computed as a contrast enhanced version of the underwater image after a noise reduction operation is performed.
2.1.1 Color Balancing of the Inputs
Color balancing is an important processing step that aims to enhance the image appearance by discarding unwanted color casts, due to various illuminants. In water deeper than 30 ft, color balancing suffers from noticeable effects since the absorbed colors are difficult to be restored. Additionally, underwater scenes present significant lack of contrast due to the poor light propagation in this type of medium.
Under- and over-contrast occur in an underwater image whereas the amount of pixels is cumulatively concentrated at low and high intensity levels. Hence, stretching and clip-limit processes are applied to the image histogram of respective regions to prevent under- and over-contrast effects. We employed Simplest Color Balance method to implement this.
The idea is that in a well balanced photo, the brightest color should be white and the darkest black. Thus, we can remove the color cast from an image by scaling the histograms of each of the R, G, and B channels so that they span the complete 0-255 scale. In contrast to the other color balancing algorithms, this method does not separate the estimation and adaptation steps.In order to deal with outliers, Simplest Color Balance saturates a certain percentage of the image's bright pixels to white and dark pixels to black. The saturation level is an adjustable parameter that affects the quality of the output. Values around 0.01 are typical. Figure 2 shows the histogram of different channels after this step. Observe that the histograms has been stretched.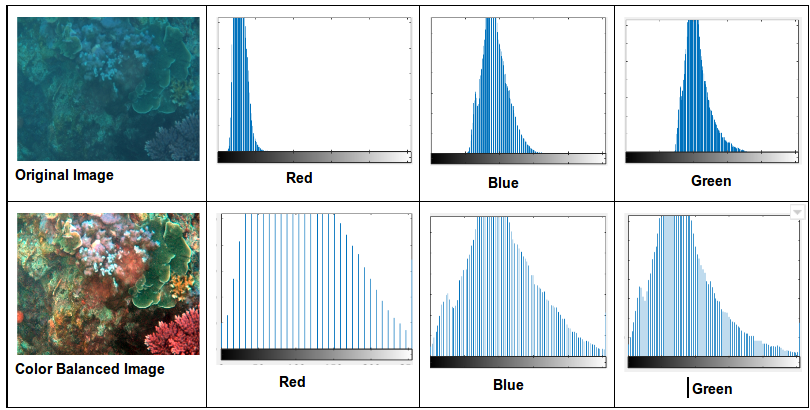
Under- and over-contrast occur in an underwater image whereas the amount of pixels is cumulatively concentrated at low and high intensity levels. Hence, stretching and clip-limit processes are applied to the image histogram of respective regions to prevent under- and over-contrast effects. We employed Simplest Color Balance method to implement this.
The idea is that in a well balanced photo, the brightest color should be white and the darkest black. Thus, we can remove the color cast from an image by scaling the histograms of each of the R, G, and B channels so that they span the complete 0-255 scale. In contrast to the other color balancing algorithms, this method does not separate the estimation and adaptation steps.In order to deal with outliers, Simplest Color Balance saturates a certain percentage of the image's bright pixels to white and dark pixels to black. The saturation level is an adjustable parameter that affects the quality of the output. Values around 0.01 are typical. Figure 2 shows the histogram of different channels after this step. Observe that the histograms has been stretched.

Figure 2: Histogram (input and output) in each channel after this step
2.1.2 Contrast Limited Adaptive Histogram Equalization
Due to the impurities and the special illumination conditions, underwater images are noisy. Removing noise while preserving edges of an input image enhances the sharpness and may be accomplished by different strategies such as median filtering, anisotropic diffusion and bilateral filtering. The bilateral filter is one of the common solutions being an non-iterative edge-preserving smoothing filter that has proven usefull for several problems such as tone mapping, mesh smoothing and dual photography enhancement.
In the fusion framework, the second input is computed from the noise-free and color corrected version of the original image. This input is designed in order to reduce the degradation due to volume scattering. To achieve an optimal contrast level of the image, the second input is obtained by applying the classical contrast local adaptive histogram equalization. To generate the second derived image common global operators can be applied as well. Since these are defined as some parametric curve, they need to be either specified by the user or to be estimated from the input image. Commonly, the improvements obtained by these operators in different regions are done at the expense of the remaining regions.The local adaptive histogram was opted since it works in a fully automated manner while the level of distortion is minor. This technique expands the contrast of the feature of interest in order to simultaneously occupy a larger portion of the intensity range than the initial image. The enhancement is obtained since the contrast between adjacent structures is maximally portrayed. To compute this input several more complex methods, such as the gradient domains or gamma correction multi-scale Retinex (MSR), may be used as well.
In the fusion framework, the second input is computed from the noise-free and color corrected version of the original image. This input is designed in order to reduce the degradation due to volume scattering. To achieve an optimal contrast level of the image, the second input is obtained by applying the classical contrast local adaptive histogram equalization. To generate the second derived image common global operators can be applied as well. Since these are defined as some parametric curve, they need to be either specified by the user or to be estimated from the input image. Commonly, the improvements obtained by these operators in different regions are done at the expense of the remaining regions.The local adaptive histogram was opted since it works in a fully automated manner while the level of distortion is minor. This technique expands the contrast of the feature of interest in order to simultaneously occupy a larger portion of the intensity range than the initial image. The enhancement is obtained since the contrast between adjacent structures is maximally portrayed. To compute this input several more complex methods, such as the gradient domains or gamma correction multi-scale Retinex (MSR), may be used as well.
2.2. Weights of the Fusion Process
The design of the weight measures needs to consider the desired appearance of the restored output.The image restoration is tightly correlated with the color appearance, and as a result the measurable values such as salient features, local and global contrast or exposedness are difficult to integrate by naive per pixel blending, without risking to introduce artifacts. Higher values of the weight determines that a pixel is advantaged to appear in the final image.
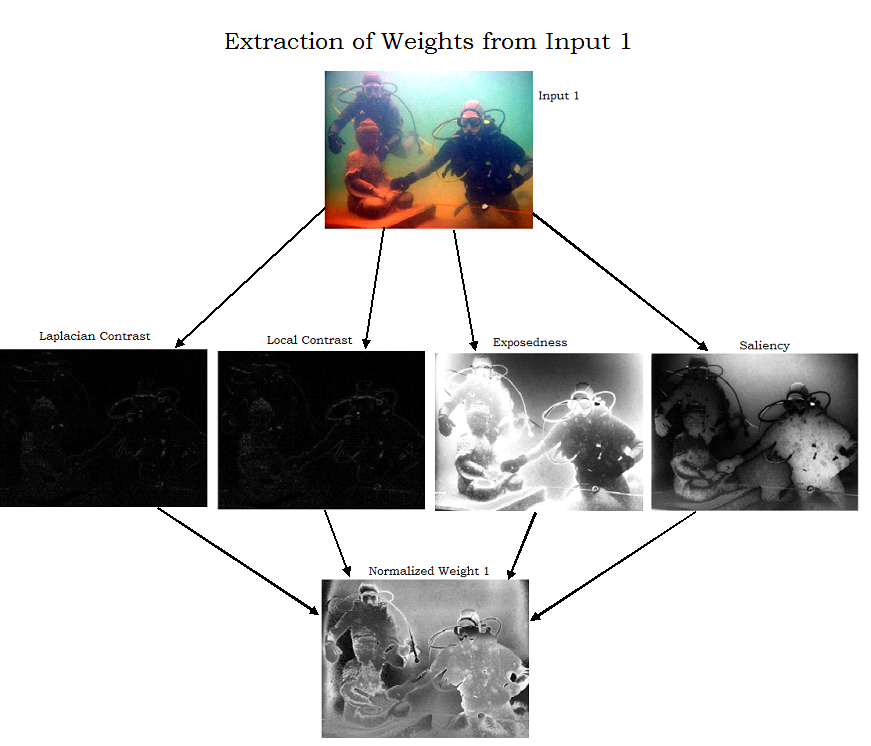
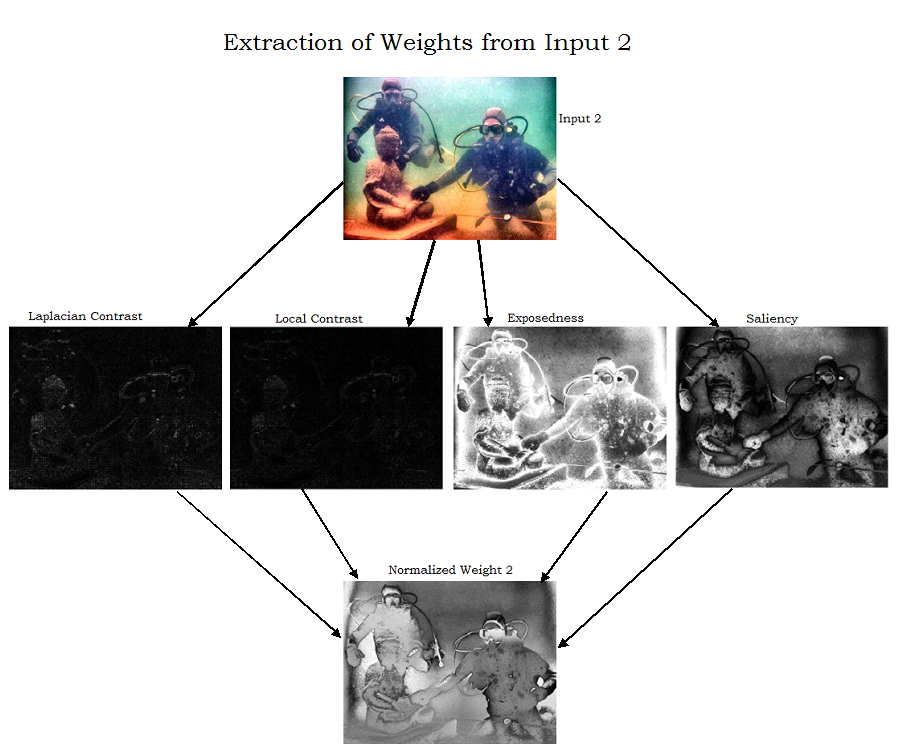
Laplacian contrast weight (WL ) deals with global contrast by applying a Laplacian filter on each input luminance channel and computing the absolute value of the filter result. This straightforward indicator was used in different applications such as tone mapping and extending depth of field since it assigns high values to edges and texture. For the underwater restoration task, however, this weight is not sufficient to recover the contrast, mainly because it can not distinguish between a ramp and flat regions. To handle this problem, an additional contrast measurement is used that independently assess the local distribution.
Local contrast weight (WLC ) comprises the relation between each pixel and its neighborhoods average. The impact of this measure is to strengthen the local contrast appearance since it advantages the transitions mainly in the highlighted and shadowed parts of the second input. The (WLC ) is computed as the standard deviation between pixel luminance level and the local average of its surrounding region:
where Ik represents the luminance channel of the input and the Iωhck represents the low-passed version of it. The filtered version Iωhck is obtained by employing a small 5 X 5( (1/16)[1, 4, 6, 4, 1]) separable binomial kernel with the high frequency cut-off value ωhc = π/2.75. For small kernels the binomial kernel is a good approximation of its Gaussian counterpart, and it can be computed more effectively.
Saliency weight (WS ) aims to emphasize the discriminating objects that lose their prominence in the underwater scene. To measure this quality, the saliency algorithm of Achanta et al. was employed. This computationally efficient saliency algorithm is straightforward to be implemented being inspired by the biological concept of center-surround contrast. However, the saliency map tends to favor highlighted areas. To increase the accuracy of results, the exposedness map was introduced to protect the mid tones that might be altered in some specific cases.
Exposedness weight (WE ) evaluates how well a pixel is exposed. This assessed quality provides an estimator to preserve a constant appearance of the local contrast, that ideally is neither exaggerated nor understated. Commonly, the pixels tend to have a higher exposed appearance when their normalized values are close to the average value of 0.5. This weight map is expressed as a Gaussian-modeled distance to the average normalized range value (0.5):
where Ik (x, y) represents the value of the pixel location (x, y) of the input image Ik , while the standard deviation is set to σ = 0.25. This map will assign higher values to those tones with a distance close to zero, while pixels that are characterized by larger distances, are associated with the over- and under- exposed regions. In consequence, this weight tempers the result of the saliency map and produces a well preserved appearance of the fused image.
To yield consistent results, we employ the normalized weight values ϒ (for an input k the normalized weight is computed as ϒk = Wk /Σk=1K Wk ), by constraining that the sum at each pixel location of the weight maps W equals one.
Laplacian contrast weight (WL ) deals with global contrast by applying a Laplacian filter on each input luminance channel and computing the absolute value of the filter result. This straightforward indicator was used in different applications such as tone mapping and extending depth of field since it assigns high values to edges and texture. For the underwater restoration task, however, this weight is not sufficient to recover the contrast, mainly because it can not distinguish between a ramp and flat regions. To handle this problem, an additional contrast measurement is used that independently assess the local distribution.
Local contrast weight (WLC ) comprises the relation between each pixel and its neighborhoods average. The impact of this measure is to strengthen the local contrast appearance since it advantages the transitions mainly in the highlighted and shadowed parts of the second input. The (WLC ) is computed as the standard deviation between pixel luminance level and the local average of its surrounding region:
WLC(x, y ) = ||Ik - Iωhck||
where Ik represents the luminance channel of the input and the Iωhck represents the low-passed version of it. The filtered version Iωhck is obtained by employing a small 5 X 5( (1/16)[1, 4, 6, 4, 1]) separable binomial kernel with the high frequency cut-off value ωhc = π/2.75. For small kernels the binomial kernel is a good approximation of its Gaussian counterpart, and it can be computed more effectively.
Saliency weight (WS ) aims to emphasize the discriminating objects that lose their prominence in the underwater scene. To measure this quality, the saliency algorithm of Achanta et al. was employed. This computationally efficient saliency algorithm is straightforward to be implemented being inspired by the biological concept of center-surround contrast. However, the saliency map tends to favor highlighted areas. To increase the accuracy of results, the exposedness map was introduced to protect the mid tones that might be altered in some specific cases.
Exposedness weight (WE ) evaluates how well a pixel is exposed. This assessed quality provides an estimator to preserve a constant appearance of the local contrast, that ideally is neither exaggerated nor understated. Commonly, the pixels tend to have a higher exposed appearance when their normalized values are close to the average value of 0.5. This weight map is expressed as a Gaussian-modeled distance to the average normalized range value (0.5):
WE(x, y) = exp((-(Ik(x, y) - 0.5)2)/(2σ2))
where Ik (x, y) represents the value of the pixel location (x, y) of the input image Ik , while the standard deviation is set to σ = 0.25. This map will assign higher values to those tones with a distance close to zero, while pixels that are characterized by larger distances, are associated with the over- and under- exposed regions. In consequence, this weight tempers the result of the saliency map and produces a well preserved appearance of the fused image.
To yield consistent results, we employ the normalized weight values ϒ (for an input k the normalized weight is computed as ϒk = Wk /Σk=1K Wk ), by constraining that the sum at each pixel location of the weight maps W equals one.
Figure 3: The two inputs derived from the original image and the corresponding normalized weight maps.
2.3. Multi-scale Fusion Process
The enhanced image version R(x, y) is obtained by fusing the defined inputs with the weight measures at every pixel location (x, y):
where Ik symbolizes the input (k is the index of the inputs K = 2 in this case) that is weighted by the normalized weight maps ϒk. The normalized weights ϒ are obtained by normalizing over all k weight maps W in order that the value P of each pixel (x, y) to be constrained by unity value( ϒk = 1).
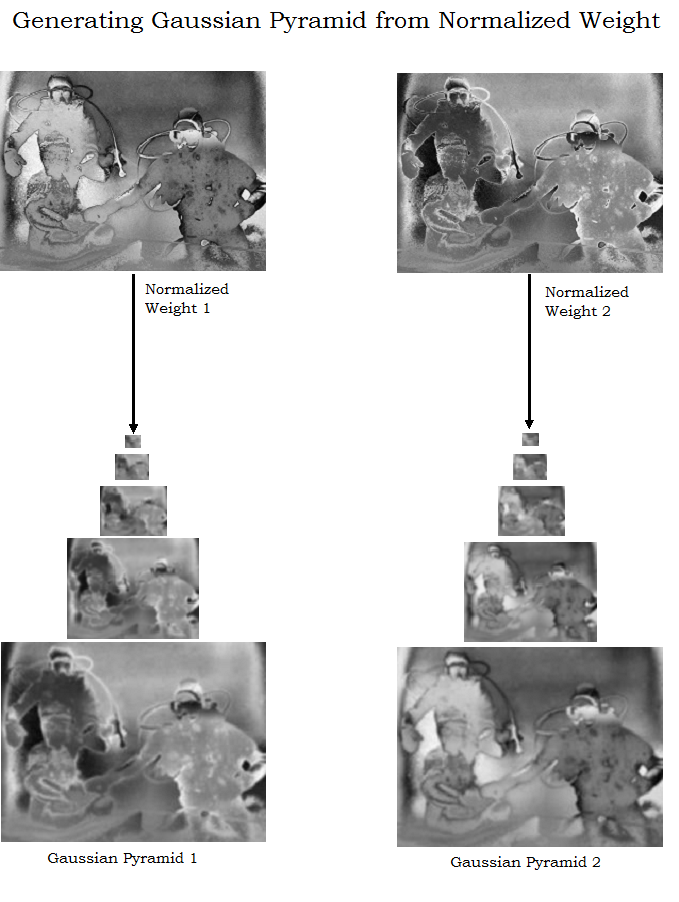
A common solution to overcome this limitation is to employ multi-scale linear or non-linear filters. The class of non-linear filters are more complex and has shown to add only insignificant improvement for this task . Since it is straightforward to implement and computationally efficient, in this experiments the classical multi-scale Laplacian pyramid decomposition has been embraced. In this linear decomposition, every input image is represented as a sum of patterns computed at different scales based on the Laplacian operator. The inputs are convolved by a Gaussian kernel, yielding a low pass filtered versions of the original. In order to control the cut-off frequency, the standard deviation is increased monotonically. To obtain the different levels of the pyramid, initially we need to compute the difference between the original image and the low pass filtered image. From there on, the process is iterated by computing the difference between two adjacent levels of the Gaussian pyramid. The resulting representation, the Laplacian pyramid, is a set of quasi-bandpass versions of the image.
In this case, each input is decomposed into a pyramid by applying the Laplacian operator to different scales. Similarly, for each normalized weight map ϒ a Gaussian pyramid is computed. Considering that both the Gaussian and Laplacian pyramids have the same number of levels, the mixing between the Laplacian inputs and Gaussian normalized weights is performed at each level independently yielding the fused pyramid:
where l represents the number of the pyramid levels (typically the number of levels is 5), L{I} is the Laplacian version of the input I, and G W̄ represents the Gaussian version of the normalized weight map ϒ . This step is performed successively for each pyramid layer, in a bottom-up manner. The restored output is obtained by summing the fused contribution of all inputs.
The Laplacian multi-scale strategy performs relatively fast representing a good trade-off between speed and accuracy. By independently employing a fusion process at every scale level the potential artifacts due to the sharp transitions of the weight maps are minimized. Multi-scale fusion is motivated by the human visual system that is primarily sensitive to local contrast changes such as edges and corners.
R(x, y)= Σk=1Kϒk(x, y) Ik(x, y)
where Ik symbolizes the input (k is the index of the inputs K = 2 in this case) that is weighted by the normalized weight maps ϒk. The normalized weights ϒ are obtained by normalizing over all k weight maps W in order that the value P of each pixel (x, y) to be constrained by unity value( ϒk = 1).
A common solution to overcome this limitation is to employ multi-scale linear or non-linear filters. The class of non-linear filters are more complex and has shown to add only insignificant improvement for this task . Since it is straightforward to implement and computationally efficient, in this experiments the classical multi-scale Laplacian pyramid decomposition has been embraced. In this linear decomposition, every input image is represented as a sum of patterns computed at different scales based on the Laplacian operator. The inputs are convolved by a Gaussian kernel, yielding a low pass filtered versions of the original. In order to control the cut-off frequency, the standard deviation is increased monotonically. To obtain the different levels of the pyramid, initially we need to compute the difference between the original image and the low pass filtered image. From there on, the process is iterated by computing the difference between two adjacent levels of the Gaussian pyramid. The resulting representation, the Laplacian pyramid, is a set of quasi-bandpass versions of the image.
In this case, each input is decomposed into a pyramid by applying the Laplacian operator to different scales. Similarly, for each normalized weight map ϒ a Gaussian pyramid is computed. Considering that both the Gaussian and Laplacian pyramids have the same number of levels, the mixing between the Laplacian inputs and Gaussian normalized weights is performed at each level independently yielding the fused pyramid:
Rl(x, y)= Σk=1KGl{ϒk(x, y)} Ll{Ik(x, y)}
where l represents the number of the pyramid levels (typically the number of levels is 5), L{I} is the Laplacian version of the input I, and G W̄ represents the Gaussian version of the normalized weight map ϒ . This step is performed successively for each pyramid layer, in a bottom-up manner. The restored output is obtained by summing the fused contribution of all inputs.
The Laplacian multi-scale strategy performs relatively fast representing a good trade-off between speed and accuracy. By independently employing a fusion process at every scale level the potential artifacts due to the sharp transitions of the weight maps are minimized. Multi-scale fusion is motivated by the human visual system that is primarily sensitive to local contrast changes such as edges and corners.
3. Experiments & Results

Figure 4: Comparision of outputs of MultiFusion technique and Histogram Equalization Method
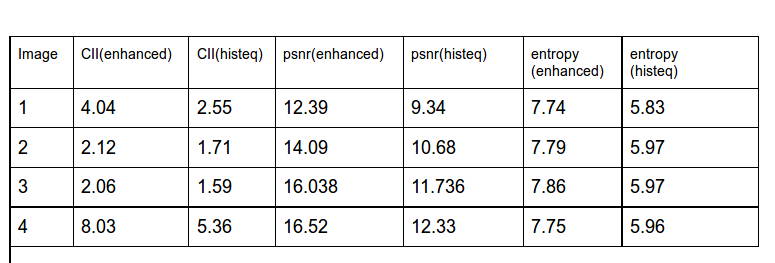
Figure 5: Quantitative analysis on several images using image quality index
3.1 Dataset Description
3.2 Discussion
In this section, we demonstrate the results obtained using the proposed algorithm. In addition to it, we compared the obtained
results with already present method namely Histogram Equalisation (HE). Quantitative analysis is done using the image
quality index, called Entropy (also called Average Information Content). The information content is related to the number of binary decisions
required to find the information. The number of binary decisions (number of questions whose answer is yes/no) required to
find the correct element in a set of N elements is:
In general, the elements are not equally likely; they have different probabilities, pi. Tribus (1961) then generalises the formula
here above by introducing the concept of ”surprisal hi”.
On this basis, Shannon introduced the uncertainty measure (also called entropy, which is the average of all surprisals hi
weighted by their occurrence pi
Quantitative comparison of images was performed on the basis of the average information content (AIC) measure. For images,
it can be written more precisely as:
where p(gk) is the PDF value for the kth gray level. In general, AIC increases with an increase in the information content of the image. In other words, a higher score indicates a richer, more detailed image. Figure 4 shows the AIC values of different images and 2 methods.
CII is the most important benchmark to compare the performance of various image enhancement techniques. It can be measured as a ratio of local contrast of final and input images. It can be represented by following equation-
where A is the average value of the local contrast measured with 3 × 3 window.Aproposed and Aoriginal are the average values of the local contrast in the output and original images, respectively. If the value of CII increases, then it shows improvement in contrast of an image.
nq= -log2N = -log2p
hi= -log2pi
H = Σipihi = -Σipilog2pi
AIC = Σk = 0L-1p(gk)log2(p(gk))
CII is the most important benchmark to compare the performance of various image enhancement techniques. It can be measured as a ratio of local contrast of final and input images. It can be represented by following equation-
CII = Aproposed/Aoriginal
4. Conclusions
4.1 Summary
Our approach has been extensively tested for real underwater images. In figure 3 is presented a direct comparison between the result of our technique and the result of histogram equalization. Compared with previous strategies, our method is straightforward to be applied since it does not require additional information such as scene depth map, hardware or special camera settings. The fusion inputs are easily to be derived from the initial image using mainly existing enhancement methods. Due to the defined weights, each pixel contribution to the final result is simply to be estimated. Additionally, the multi-scale approach secures that the abrupt changes of the weights are not visible in the final composition. Similar as the existing underwater restoring strategies, a main limitation of our method is represented by the fact that the noise contribution may be amplified significantly with the depth yielding undesired appearance of the distant regions.
We presented a fusion-based approach to restore underwater images. We demonstrate that by defining proper inputs and weights derived from the original degraded image they can be effectively blend in a multi-scale fashion to improve considerably the visibility range of the input underwater images.
We presented a fusion-based approach to restore underwater images. We demonstrate that by defining proper inputs and weights derived from the original degraded image they can be effectively blend in a multi-scale fashion to improve considerably the visibility range of the input underwater images.
4.2 Future Extensions
The alogorithm can be improved so that it'd take less time for computation. Also, It could be tested on videos and atmospheric hazed images.
5. Application
Image dehazing is the process of removing the haze and fog effects from the spoilt images. Because of similarities between hazy and underwater environments due to the light scattering process, we found our strategy appropriate for this challenging task. However, as explained previously, since the underwater light propagation is more complex we believe that image dehazing could be seen as a subclass of the underwater image restoration problem. Comparative results with state-of-the-art single image dehazing techniques are shown in Figure 5.


Figure 5: Our method on Atmospheric hazed images
6. Campus Galary



